what does it mean for a function to be single valued

What is a Function?

A function relates an input to an output.

It is like a machine that has an input and an output.

And the output is related somehow to the input.

f(x)	"f(x) = ... " is the archetype manner of writing a function. And there are other ways, equally you volition come across!

Input, Relationship, Output

Nosotros will see many ways to think about functions, simply there are always three principal parts:

• The input
• The relationship
• The output

Example: "Multiply by two" is a very simple function.

Here are the iii parts:

Input	Relationship	Output
0	× 2	0
ane	× ii	2
7	× ii	14
10	× 2	20
...	...	...

For an input of l, what is the output?

Some Examples of Functions

• 10² (squaring) is a part
• x³+one is besides a function
• Sine, Cosine and Tangent are functions used in trigonometry
• and there are lots more!

Merely we are not going to look at specific functions ...
... instead we will look at the general thought of a function.

Names

First, it is useful to requite a part a proper noun.

The most mutual proper name is " f ", but we can have other names like " g " ... or fifty-fifty " marmalade " if we want.

But let's utilize "f":

We say "f of x equals x squared"

what goes into the office is put inside parentheses () after the name of the office:

So f(ten) shows us the office is called " f ", and " x " goes in

And we commonly encounter what a part does with the input:

f(x) = x² shows us that role " f " takes " 10 " and squares it.

Example: with f(ten) = x² :

• an input of iv
• becomes an output of 16.

In fact nosotros can write f(four) = xvi.

The "x" is Just a Place-Holder!

Don't get likewise concerned most "10", it is just in that location to show united states where the input goes and what happens to it.

It could be anything!

Then this function:

f(x) = 1 - x + 10ⁱⁱ

Is the same function as:

• f(q) = 1 - q + q²
• h(A) = 1 - A + A²
• w(θ) = i - θ + θ²

The variable (x, q, A, etc) is simply in that location and then we know where to put the values:

f(2) = one - 2 + 2 ² = 3

Sometimes There is No Function Proper noun

Sometimes a function has no name, and nosotros see something like:

y = 10ⁱⁱ

But in that location is still:

• an input (x)
• a relationship (squaring)
• and an output (y)

Relating

At the top we said that a part was like a machine. But a function doesn't really have belts or cogs or whatsoever moving parts - and it doesn't actually destroy what we put into it!

A function relates an input to an output.

Saying "f(iv) = 16" is like proverb 4 is somehow related to xvi. Or iv → 16

Example: this tree grows 20 cm every year, so the height of the tree is related to its age using the role h :

h(age) = age × xx

So, if the age is 10 years, the height is:

h(ten) = 10 × 20 = 200 cm

Here are some instance values:

age	h(age) = historic period × twenty
0	0
1	twenty
three.2	64
15	300
...	...

What Types of Things Do Functions Procedure?

"Numbers" seems an obvious answer, only ...

	... which numbers? For example, the tree-height function h(historic period) = historic period×20 makes no sense for an age less than zippo.
	... it could also exist letters ("A"→"B"), or ID codes ("A6309"→"Pass") or stranger things.

And so we need something more powerful, and that is where sets come in:

A set is a collection of things. Here are some examples: Gear up of even numbers: {..., -4, -ii, 0, 2, 4, ...} Ready of dress: {"hat","shirt",...} Set of prime number numbers: {two, three, 5, 7, 11, 13, 17, ...} Positive multiples of 3 that are less than 10: {three, 6, 9}

Each individual affair in the set up (such as "4" or "hat") is called a member, or element.

So, a function takes elements of a set, and gives dorsum elements of a set up.

A Role is Special

Only a role has special rules:

• Information technology must work for every possible input value
• And it has only i relationship for each input value

This can be said in i definition:

Formal Definition of a Part

A function relates each element of a set
with exactly one element of another set
(maybe the same set).

The Two Of import Things!

one.	"...each element..." means that every chemical element in X is related to some element in Y. Nosotros say that the function covers X (relates every element of it). (But some elements of Y might not exist related to at all, which is fine.)

ii.	"...exactly 1..." ways that a part is single valued . It will not requite back two or more than results for the same input. And then "f(2) = 7 or 9" is not correct!

"One-to-many" is not allowed, just "many-to-ane" is allowed:
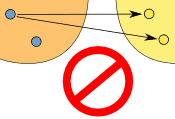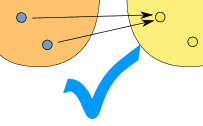(one-to-many)		(many-to-one)
This is Not OK in a function		But this is OK in a office

When a relationship does non follow those two rules then it is not a function ... it is still a human relationship, just non a function.

Example: The human relationship x → x^two

Could also be written every bit a tabular array:

X: x	Y: xtwo
three	nine
1	1
0	0
4	16
-4	16
...	...

It is a function, because:

• Every chemical element in 10 is related to Y
• No element in X has two or more relationships

So it follows the rules.

(Observe how both 4 and -4 relate to 16, which is allowed.)

Instance: This human relationship is non a function:

It is a relationship, but it is not a function, for these reasons:

• Value "3" in 10 has no relation in Y
• Value "4" in X has no relation in Y
• Value "5" is related to more than one value in Y

(But the fact that "6" in Y has no relationship does not affair)

Vertical Line Examination

On a graph, the idea of single valued means that no vertical line ever crosses more than ane value.

If it crosses more than than once it is however a valid curve, simply is non a function.

Some types of functions have stricter rules, to find out more than you tin can read Injective, Surjective and Bijective

Infinitely Many

My examples have just a few values, just functions normally piece of work on sets with infinitely many elements.

Example: y = xⁱⁱⁱ

• The input set "10" is all Existent Numbers
• The output set "Y" is also all the Existent Numbers

Nosotros tin can't testify ALL the values, and then here are just a few examples:

Ten: x	Y: x3
-two	-8
-0.1	-0.001
0	0
1.1	ane.331
3	27
so on...	and so on...

Domain, Codomain and Range

In our examples higher up

• the set "10" is called the Domain,
• the set "Y" is called the Codomain, and
• the ready of elements that get pointed to in Y (the bodily values produced by the function) is called the Range.

Nosotros have a special folio on Domain, Range and Codomain if you lot desire to know more.

So Many Names!

Functions have been used in mathematics for a very long time, and lots of different names and means of writing functions take come up almost.

Here are some common terms you should get familiar with:

Example: z = 2u³ :

• "u" could exist called the "independent variable"
• "z" could be called the "dependent variable" (information technology depends on the value of u)

Example: f(4) = 16:

• "4" could be called the "argument"
• "16" could be called the "value of the function"

Example: h(year) = xx × year:

• h() is the part
• "year" could be called the "argument", or the "variable"
• a stock-still value similar "20" can be called a parameter

We oft call a part "f(10)" when in fact the role is really "f"

Ordered Pairs

And here is another manner to call up virtually functions:

Write the input and output of a function as an "ordered pair", such every bit (four,sixteen).

They are called ordered pairs because the input ever comes first, and the output 2d:

(input, output)

And then it looks like this:

( x, f(ten) )

Example:

(4,16) ways that the function takes in "4" and gives out "xvi"

Set of Ordered Pairs

A function can then be divers equally a fix of ordered pairs:

Example: {(two,4), (three,five), (7,3)} is a function that says

"ii is related to iv", "three is related to 5" and "7 is related three".

Also, notice that:

• the domain is {two,3,7} (the input values)
• and the range is {4,five,3} (the output values)

But the function has to be single valued, so nosotros likewise say

"if it contains (a, b) and (a, c), then b must equal c"

Which is just a way of saying that an input of "a" cannot produce two different results.

Case: {(2,four), (2,5), (seven,3)} is non a office because {two,iv} and {two,v} ways that ii could be related to 4 or 5.

In other words it is non a function considering it is non single valued

A Benefit of Ordered Pairs

Nosotros can graph them...

... because they are also coordinates!

And then a fix of coordinates is besides a role (if they follow the rules above, that is)

A Role Can be in Pieces

Nosotros tin can create functions that behave differently depending on the input value

Case: A role with two pieces:

• when ten is less than 0, it gives 5,
• when ten is 0 or more than it gives x²

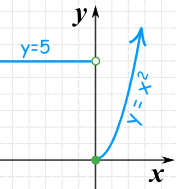Here are some example values: x y -3 5 -one 5 0 0 2 4 iv 16 ... ...

Read more than at Piecewise Functions.

Explicit vs Implicit

1 last topic: the terms "explicit" and "implicit".

Explicit is when the function shows us how to get straight from x to y, such as:

y = x³ − three

When nosotros know x, we can find y

That is the classic y = f(x) style that we often piece of work with.

Implicit is when it is not given directly such as:

x² − 3xy + y³ = 0

When we know x, how do nosotros find y?

It may be hard (or impossible!) to become directly from x to y.

"Implicit" comes from "implied", in other words shown indirectly.

Graphing

• The Function Grapher tin only handle explicit functions,
• The Equation Grapher tin can handle both types (but takes a little longer, and sometimes gets information technology wrong).

Conclusion

• a function relates inputs to outputs
• a function takes elements from a fix (the domain) and relates them to elements in a fix (the codomain).
• all the outputs (the actual values related to) are together called the range
• a function is a special type of relation where:
  • every element in the domain is included, and
  • any input produces but one output (not this or that)
• an input and its matching output are together called an ordered pair
• then a function tin besides exist seen as a set up of ordered pairs

5571, 5572, 535, 5207, 5301, 1173, 7281, 533, 8414, 8430

monizupos1990.blogspot.com

Source: https://www.mathsisfun.com/sets/function.html